I rompicapi geometrici da sempre rappresentano una straordinaria palestra per l’ingegno, stimolando la mente e accendendo la curiosità di chi ama le sfide intellettuali. Questi enigmi, infatti, offrono occasioni uniche per mettere alla prova le proprie capacità di ragionamento e di problem solving, coinvolgendo competenze logiche e visive di vario genere. Tra i tanti, alcuni rompicapi apparentemente semplici hanno saputo mettere in difficoltà anche esperti e studiosi, rivelando quanto sia sottile il confine tra intuizione e inganno.
Il problema dei nove punti
Tra i rompicapi geometrici più celebri spicca il cosiddetto problema dei nove punti. Questo enigma prevede la disposizione di nove punti su un piano, organizzati in una griglia 3 x 3. La sfida consiste nel collegare tutti i nove punti utilizzando soltanto quattro segmenti di linea retta, senza mai sollevare la penna dal foglio e senza ripassare su alcun segmento già tracciato.

All’apparenza, il problema sembra di facile soluzione, ma in realtà molti si trovano in difficoltà nel trovare una risposta che rispetti tutte le condizioni richieste. La chiave sta nel saper andare oltre i limiti autoimposti: spesso si tenta di collegare i punti restando confinati all’interno della griglia, ma questa restrizione non è presente nelle istruzioni.
La soluzione, infatti, richiede di estendere i segmenti oltre i confini della griglia 3 x 3, che rappresenta solo un limite mentale. Nulla vieta di tracciare linee che escano dall’area delimitata dai punti: è proprio questa la dimostrazione di come il pensiero laterale sia fondamentale per risolvere il rompicapo. Solo abbandonando le consuete abitudini mentali si può arrivare alla soluzione corretta.
Il paradosso dell’area scomparsa
Un altro rompicapo geometrico di grande fama è il paradosso dell’area scomparsa. Questo enigma propone due figure che, a prima vista, sembrano identiche e composte dalle stesse tessere geometriche. Tuttavia, una delle due figure sembra avere un’area mancante rispetto all’altra, dando origine a un vero e proprio paradosso. Come si spiega questa apparente contraddizione? Ecco la soluzione al mistero dell’area scomparsa.
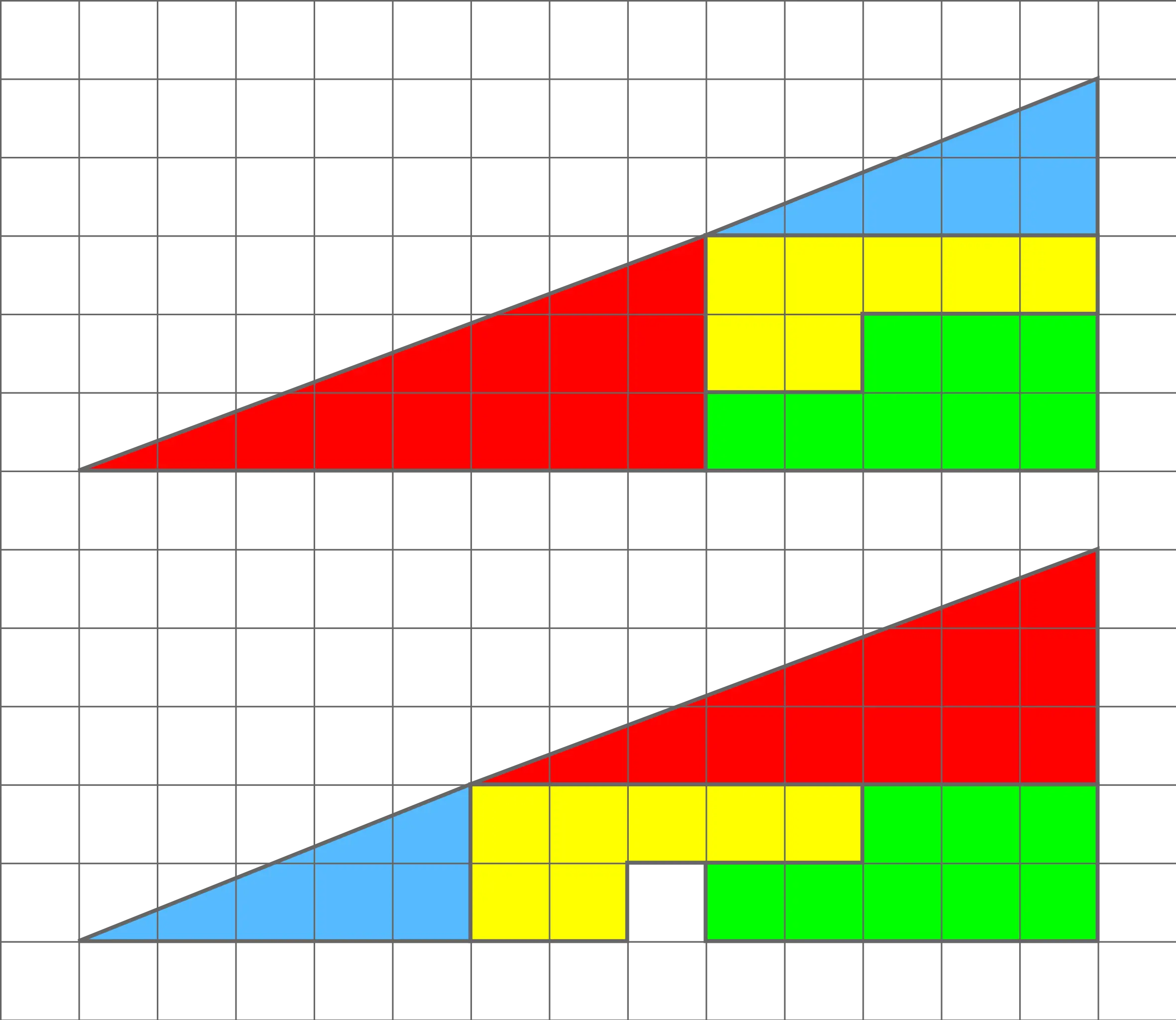
La spiegazione di questo inganno visivo risiede nel fatto che le due figure, pur essendo formate dalle stesse tessere, non sono perfettamente identiche nella disposizione. La differenza, quasi impercettibile, riguarda gli angoli e la disposizione delle tessere, che fanno sì che una figura risulti leggermente più grande dell’altra, generando così l’illusione di un’area scomparsa.
Questa sottile variazione sfugge facilmente all’occhio, rendendo il paradosso dell’area scomparsa un ottimo esempio di come la percezione visiva possa essere ingannata. Per evitare di cadere in errore, è necessario analizzare con attenzione la geometria delle figure, osservando le piccole differenze negli angoli e nelle dimensioni che possono avere un impatto decisivo.
La torre di Hanoi
Tra i rompicapi geometrici più noti figura anche la torre di Hanoi, conosciuta anche come Torre di Lucas dal nome del suo inventore. Questo enigma consiste in una serie di dischi di dimensioni diverse, impilati in ordine decrescente su un paletto, con l’obiettivo di trasferirli su un altro paletto mantenendo sempre l’ordine dal più grande al più piccolo.

Un terzo paletto funge da supporto temporaneo, ma la regola fondamentale impone che un disco più grande non possa mai essere posizionato sopra uno più piccolo. La soluzione di questo rompicapo è di natura matematica e si basa sul calcolo del numero minimo di mosse necessarie per completare il trasferimento: la formula è 2n – 1, dove “n” rappresenta il numero dei dischi. Ad esempio, per tre dischi sono richieste almeno sette mosse.
La torre di Hanoi ha affascinato generazioni di appassionati fin dalla sua invenzione, avvenuta nel 1883 ad opera del matematico francese Édouard Lucas. A questo rompicapo è legata anche una suggestiva leggenda: si narra che in un antico tempio indù, dei monaci siano impegnati da secoli nella soluzione del problema, e che il destino del mondo sia legato al completamento della loro impresa.
Il valore dei rompicapi geometrici
I rompicapi geometrici rappresentano strumenti didattici di grande valore, in quanto favoriscono lo sviluppo del pensiero critico e delle capacità di ragionamento logico. La loro risoluzione richiede di analizzare la situazione, formulare ipotesi e individuare strategie, attivando un processo mentale che stimola la riflessione e la creatività.

Questo tipo di esercizio mentale promuove un apprendimento attivo e consente di comprendere concetti matematici e geometrici in modo intuitivo, con benefici che si riflettono su numerosi processi cognitivi. Affrontare questi enigmi costringe la mente a operare in condizioni di incertezza, stimolando l’autonomia, la gestione dell’errore e la capacità di riformulare strategie efficaci per arrivare alla soluzione.
Tali competenze contribuiscono a sviluppare una maggiore flessibilità mentale, utile non solo in ambito scolastico o professionale, ma anche nella vita quotidiana. Saper affrontare problemi complessi, valutare alternative e prendere decisioni rapide ed efficaci è fondamentale per adattarsi a situazioni nuove e trovare soluzioni innovative, imparando a gestire gli errori e a trasformarli in opportunità di crescita.









